Předmět: Zeměpis Stupeň školy: 2. stupeň ZŠ Region: Česko
Přemýšleli jste někdy o tom, kde leží střed Česka? Již 10 let je v místech geometrického středu u Číhoště vztyčen pamětní kámen, ale možná vás překvapí, že se nejedná o jediný možný střed naší země. Zkuste si schválně odpovědět na otázku, jaké místo považujete za střed Česka a jak byste takový bod našli, a uvidíte, jak široká škála názorů se objeví.
Problematice hledání středů Česka se ve svém článku v Geografických rozhledech (roč. 2016/2017, č. 3) věnují Jan D. Bláha a Martin Dolejš z PřF UJEP v Ústí nad Labem. Svůj článek nám poskytli a tak vám, díky nim, tuto problematiku trochu poodkryjeme.
Podle způsobu odvození lze v první fázi rozlišovat středy zkonstruované (např. střed zkonstruovaný na základě vzdálenosti od hranic daného území), středy území stanovené na základě určitých kritérií (např. astronomický, kulturní) a středy spočítané na základě fyzicko-geografických či sociálně-geografických jevů (např. populační či výškový geometrický střed). Někdy bývají středy odvozené ze sociálních jevů označovány spíše jako centra.
Obecně má na středy území vliv celá řada faktorů. Zcela zásadní je samotné určení hranic území (regionu, administrativní jednotky, státu, kontinentu atd.). V tomto ohledu je například téměř nemožné přesně stanovit střed Evropy, neboť její vymezení není ustálené. Mohlo by se zdát, že v případě Česka je výše uvedený problém vyřešen. Nelze však opomenout jeden z faktorů, a to je vývoj a změna území. Nedávno byla kupříkladu otevřena znovu otázka česko-polské hranice, která byla v padesátých letech 20. století za účelem efektivnější ostrahy napřímena a Polsko přitom přišlo o cca 400 hektarů pozemků (mj. Kovařík, 2016). V případě, že by Vláda ČR kdykoli v budoucnosti schválila změnu území, bude to mít bezesporu vliv na některé z dále uvedených středů Česka.
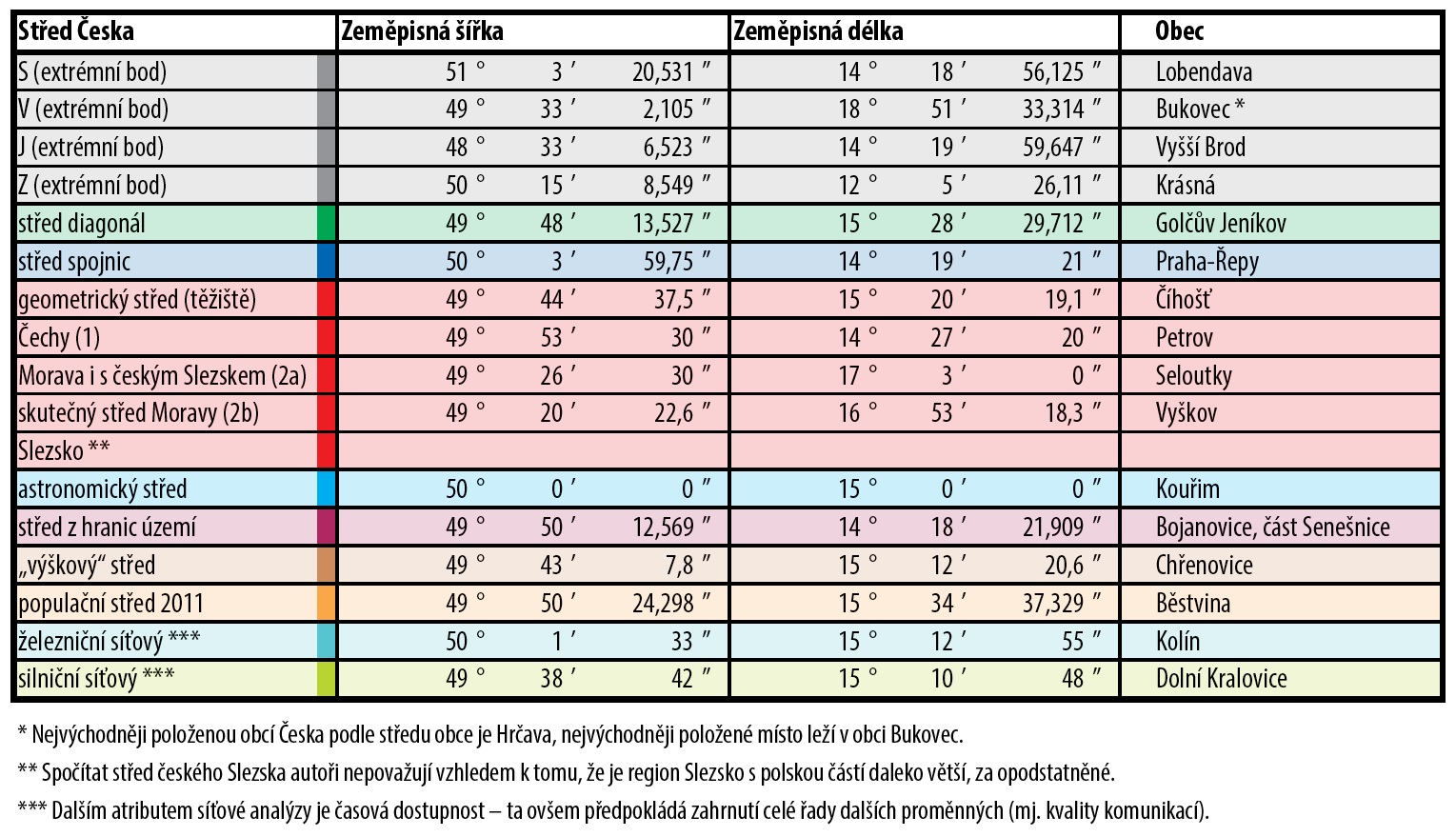
Dalším významným faktorem je otázka přesnosti a způsobu (metody) měření. Dokazují to například odlišné výsledky zjištění geometrického středu (těžiště plochy vymezené hranicemi) od S. Böhma, R. Čapka, V. Fialy či L. Fofonky. Přes různé metody tito autoři dosáhli poměrně přesných výsledků – Čapkův střed se liší cca o 1 km, Fialův dokonce jen o necelých 500 m od oficiálně uznaného středu, který zaměřil geodet L. Fofonka (2005). Ten vycházel z předpokladu, že těžiště uzavřeného nepravidelného mnohoúhelníku lze spočítat jako vážený průměr těžišť trojúhelníků, do nichž je rozdělena celá plocha (pro území Česka použil celkem 2 834 trojúhelníků). Váhou každého jednoho těžiště je přitom plocha trojúhelníku, k němuž těžiště náleží. Výsledkem jsou souřadnice bodu, který může, ale nemusí ležet uvnitř dané plochy (v Česku leží právě v obci Číhošť).
Nabízí se i jednodušší vysvětlení, jak zkonstruovat těžiště plochy. Ke stejnému bodu bychom hypoteticky dospěli tak, že bychom vyřízli nezkreslenou plochu území Česka (např. z dřevěné desky) a zjistili alespoň dvě těžnice této plochy (např. zavěšením olovnice na okraj plochy). Těžiště pak leží v průsečíku těžnic plochy.
Problém může nastat u přímořských států. U nich je totiž třeba zjišťovat těžiště hned pro tři různá území: pro pevninu bez ostrovů, pro veškerou souš včetně ostrovů a pro celkové území včetně teritoriálních vod. Stejně tak u států s děleným (např. Angola) či perforovaným územím (např. Republika Jižní Afrika) je třeba počítat s odpovídající plochou.
Ačkoliv je v případě těžiště využito různých výpočtů, principiálně se jedná o zkonstruovaný střed. Dalším příkladem zkonstruovaného středu či významného bodu je průsečík nejkratších spojnic extrémních bodů území (spojnice nejsevernějšího a nejjižnějšího bodu a spojnice nejvýchodnějšího a nejzápadnějšího bodu). U některých pravidelných území ohraničených poledníkem, rovnoběžkou či jejich dvojicemi může být takových spojnic nekonečně mnoho (viz např. stát Colorado). Není bez zajímavosti, že se tento průsečík v případě Česka nachází na území Prahy, konkrétně v městské části Praha-Řepy.
Od extrémních bodů území je odvozen také střed diagonál nejmenšího pravidelného čtyřúhelníku opsaného území. Strany tohoto sférického čtyřúhelníku jsou příslušné rovnoběžky a poledníky. V případě Česka leží tento průsečík v obci Golčův Jeníkov. Oba tyto středy však obecně nemusí ležet uvnitř sledovaného území, podobně jako u těžiště totiž záleží na jeho tvaru.
Velice zajímavým bodem je střed určený na základě hranic území. Jedná se o bod, u něhož je součet všech přímých vzdáleností na hranice příslušného území největší. Pokud bychom z tohoto místa chtěli dorazit letecky co nejkratší cestou na hranice, uletěli bychom v případě Česka vzdálenost více než 104 km. Ze všech ostatních míst v Česku tak daleko na nejbližší hranice není. Toto místo leží v obci Bojanovice, v místní části Senešnice. Z principu konstrukce vyplývá, že toto místo leží vždy uvnitř území a teoreticky takových míst, která leží na tzv. střední ose území, může být i více.
Další skupinu představují středy stanovené na základě určitých kritérií. Takovým středem je i astronomický střed Česka v obci Kouřim, z něhož se u nás počítají okamžiky astronomických úkazů. O tomto místě informovala Česká astronomická společnost v roce 1995. Za další středy, nebo spíše centra, mohou být považována místa (sídla), v nichž se kumuluje např. ekonomický či kulturní potenciál společnosti. Tento potenciál se přitom určuje prostřednictvím různých kritérií (např. počtem podnikatelských subjektů, přítomností burzy, počtem kulturních památek či počtem vysokých škol). Za kulturní i ekonomické centrum Česka je dlouhodobě považována Praha.
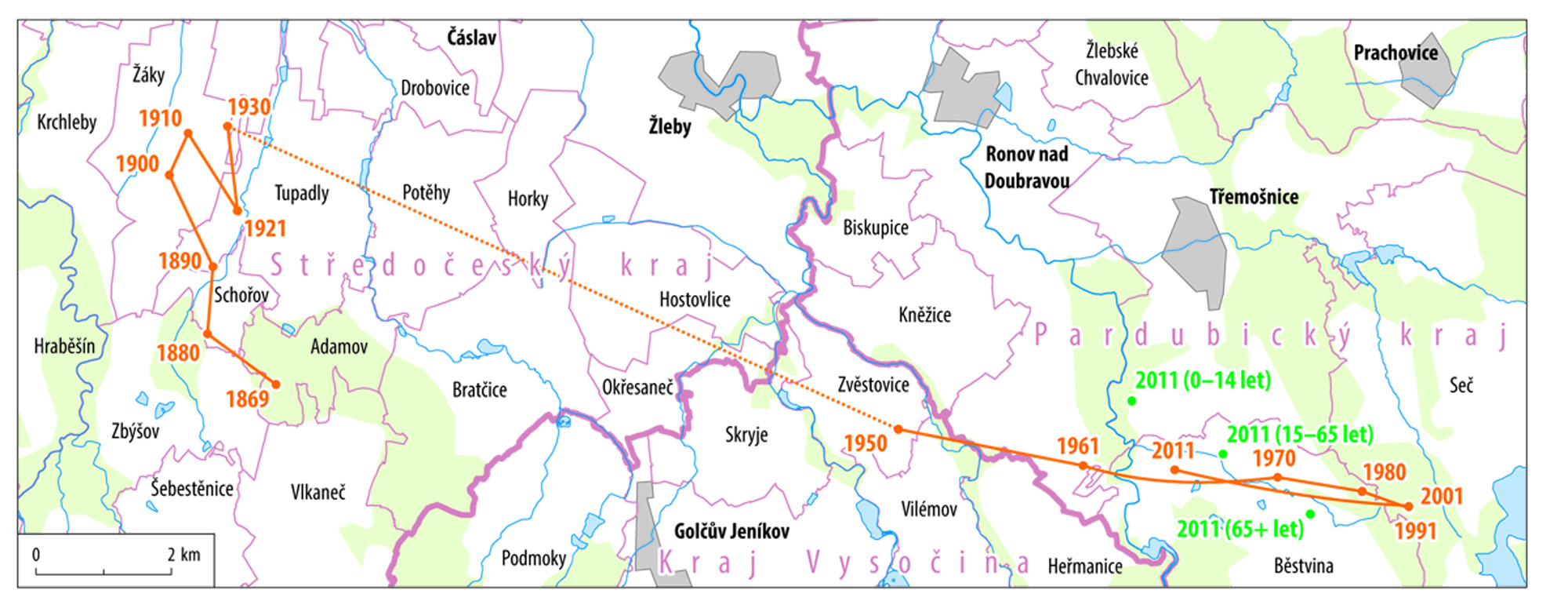
Středy spočítané na základě rozložení určitého jevu v dané ploše se určují jako těžiště bodového pole (aritmetický průměr), v němž jsou často body rozmístěny nepravidelně a mohou mít různou váhu (vážený průměr). Typickým představitelem jsou populační středy, spočítané z rozmístění sídel vážených počtem obyvatel. Sledovat u nich lze jednak vývoj v čase (posun středu), jednak různé charakteristiky populace (např. různé věkové skupiny). Interpretace vývoje a rozložení populačních středů Česka by vydala na samostatnou studii.Některé středy se počítají pomocí tzv. síťové analýzy (např. silniční a železniční střed vychází ze sítě silnic, resp. železnic). Podmínkou je, aby tyto středy ležely na síti a suma všech vzdáleností po síti spočítaná z těchto středů do všech sídel (platí pro silniční střed) nebo železničních zastávek (platí pro železniční střed) byla co nejmenší. Dalším atributem síťové analýzy může být časová dostupnost. Ta ovšem předpokládá zahrnutí celé řady dalších proměnných (mj. kvality komunikací).Poněkud odlišnou povahu mají středy vycházející z přírodních složek krajiny (fyzicko-geografické jevy). Tyto složky se obecně vyznačují kontinuitou (spojitostí) nebo diskontinuitou (ohraničeností). Zatímco kontinuita se projevuje spojitým prostorovým rozšířením jevu (např. nadmořská výška, teplota, tlak vzduchu), diskontinuita existencí přírodních jednotek (např. geologické jednotky, půdní typy) – (Balej, Anděl a kol., 2005). U kontinuálních jevů lze analýzou příslušného digitálního modelu spočítat hypotetický střed území, ačkoliv vhodnějším ukazatelem je střední hladina, resp. hodnota jevu (např. střední nadmořská výška, průměrná teplota), vyjádřená určitou izolinií. Kupříkladu střední nadmořská výška je v případě Česka vyjádřena vrstevnicí o nadmořské výšce 447 m. Přesnost výpočtu záleží především na přesnosti modelu (v případě nadmořské výšky digitálního modelu reliéfu – DMR) a hustotě bodové sítě (v případě charakteristik počasí hustotou sítě meteorologických stanic), z níž je střed počítán, tak jako u předchozích středů, v podobě těžiště.Výškový geometrický střed se nachází na území obce Chřenovice, což je vlastně těžiště zohledňující hypsografii území Česka. Tento bod byl spočítán jako vážený průměr z DMR databáze ArcČR 500 z bodové množiny o počtu 1 mil. bodů, tj. zhruba ze 13 bodů/1 km2, kde vahou byla nadmořská výška. Přesnější by byl výsledek z tzv. DMR 5G, ale pro potřeby této studie je přesnost dostačující.
Hledání středů území Česka nekončí, neboť se ukazuje, že každá metoda a každý přírodní a sociální jev přinášejí odlišný výsledek. Navíc existuje řada faktorů, které tento výsledek ovlivňují. Střed v Číhošti je tedy mylně označován jako geografický střed. Je to totiž pouze jeden ze středů, které geografové mohou odvodit z území a objektů či jevů vyskytujících se v území Česka. Autoři k prostorové analýze využili dostupná relativně podrobná data a současně moderní nástroje GIS. Přesto si uvědomují, že by bylo možné výsledky ještě zpřesňovat. Otázkou ovšem zůstává, do jaké míry to má smysl. Důležité je, aby si žáci uvědomili rozmanitost přírodní a sociální sféry, tedy i existenci téměř nekonečného množství středů území.
Balej, M., Anděl, J. a kol. (2005): Komplexní geografické hodnocení kulturní krajiny. I. díl. Tomáš Mikulenka, Ústí nad Labem, 201 s.
Bourke, P. (1988): Calculating the area and centroid of a polygon. Dostupné na http://paulbourke.net/geometry/polygonmesh.
Fiala, V. (1997): Stanovení středu území České republiky. Geodetický a kartografický obzor, 85, 11, s. 249–250.
Fofonka L. (2005): Střed České republiky. Zeměměřič, č. 5.
Hanewinkel, C., Hölzel, B. (2012): Deutschlands Mittelpunkte. Leibniz-Institut für Länderkunde, Lipsko (mapa).
Kovařík, J. (2016): Polsko chce po Česku 368 hektarů území. Právo, 7. dubna.
Semian, M. (2012): Český ráj. Ale který? Geografické rozhledy, 21, 3, s. 26–27.
Střeštík, J. (2012): Kde leží střed Čech, Moravy, České republiky a Evropy. In: Bělík, M. (ed.) Člověk ve svém pozemském a kosmickém prostředí, s. 65–71.
Vondráková, A. (2012): Určování středu území. Učební text pro potřeby UP v Olomouci.
Materiály z archivů autorů a R. Čapka.
Data: ArcČR 500, Česká astronomická společnost, Statistiky ČSÚ, ZABAGED.
Středy Česka - článek s mapou (A4 1.06 MB, .pdf)
Středy Česka - mapa (A4 482 kB, .pdf)
Posun populačního středu Česka (A4 664 kB, .pdf)
Středy Česka v tabulce (A4 378 kB, .jpg)